


 Download WORD file and JPG images of the third edition for publication
Download WORD file and JPG images of the third edition for publication
Coordinates, which consist of long sequences of digits and sometimes also letters, to precisely indicate points on the earth's surface with them, are not easy to understand for most people.
This article describes the calculation methods and the display formats as well as the historical background of the UTM coordinate system.
 "Universal Transverse Mercator" (UTM) goes back to the scientific genius Gheert de Cremer, alias Gerardus Mercator.
In the middle of the 16th century, Mercator found a way to depict the globe on a flat map that was particularly well suited for navigation.
Because Mercator's projection was a true angular (conformal) representation of the globe, sailors could plot their courses as straight lines on Mercator's map and thus, unlike other maps, navigate very easily with a compass.
"Universal Transverse Mercator" (UTM) goes back to the scientific genius Gheert de Cremer, alias Gerardus Mercator.
In the middle of the 16th century, Mercator found a way to depict the globe on a flat map that was particularly well suited for navigation.
Because Mercator's projection was a true angular (conformal) representation of the globe, sailors could plot their courses as straight lines on Mercator's map and thus, unlike other maps, navigate very easily with a compass.
The true angular UTM Coordinate System was developed in the United States after the Second World War for military and especially for navigation purposes from the Mercator projection.
In the meantime, due to general globalization, many national coordinate systems have been replaced by the globally uniform UTM Coordinate System.
There are different display formats for UTM coordinates depending on their use.
The most common display formats are explained below using examples from the transformation software TRANSDATpro developed by Killet GeoSoftware Ing.-GbR.
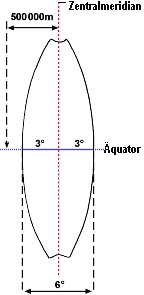
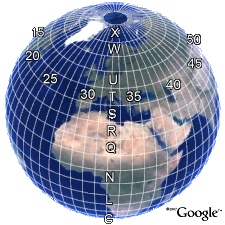 According to the UTM Coordinate System, the globe is divided into vertical UTM zones of 6 longitudes each.
These zones are arranged round the equator, to be compared with orange peels.
Starting eastwards at 177 degrees West, they are numbered from 1 to 60.
Each UTM zone is regarded as an individual Cartesian Coordinate System.
The origin for each UTM zone is the intersection of the equator with the corresponding central meridian.
The easting of the central meridian is shifted by 500.000 meters, in order to obtain exclusively positive values.
For the same reason, when being displayed on the southern hemisphere, the northing is shifted by 10.000.000 meters.
According to the UTM Coordinate System, the globe is divided into vertical UTM zones of 6 longitudes each.
These zones are arranged round the equator, to be compared with orange peels.
Starting eastwards at 177 degrees West, they are numbered from 1 to 60.
Each UTM zone is regarded as an individual Cartesian Coordinate System.
The origin for each UTM zone is the intersection of the equator with the corresponding central meridian.
The easting of the central meridian is shifted by 500.000 meters, in order to obtain exclusively positive values.
For the same reason, when being displayed on the southern hemisphere, the northing is shifted by 10.000.000 meters.
The Prime Meridian Greenwich is the exact border between the UTM zones 30 and 31.
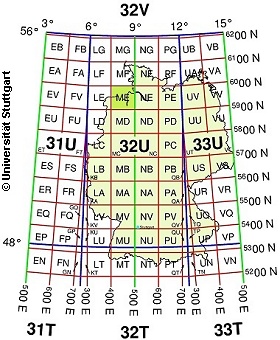
Germany, for example, is mostly located in the UTM zones 32 and 33.
There are various options to represent UTM coordinates.
By way of example, we are going to list the UTM coordinates of the beacon "Red Sand" at the mouth of the river Weser (53° 51' 18'' N / 8° 4' 54'' E) using different notations.
All notations, however, describe the same point in the Coordinate System.
| • UTM Zone Coordinates | 32439596 / 5967780 | Easting and Northing |
| • | 33045270 / 5989604 | in adjacent UTM zone |
| • MGRS/UTMref/UTM Reference System | 32UME3959667780 | Recording exact to the meter |
| • | 32UME3967 | Recording to the kilometer |
| • UTM Grid Coordinates | 32U4395965967780 | Grid coordinate |
| • Reduced UTM Coordinates | 439596 / 967780 | Reduced Easting and Northing |
| • | 439596 / 5967780 | Reduced Easting |
The examples show the multiple possibilities of UTM coordinates. Depending on the particular application, UTM coordinates with the notations listed above are used. Here, we are going to explain the exact meaning of the individual digits and letters, appearing within the coordinate. In the following, we are going to show ways to convert UTM coordinates from one display mode to another.
The most common representation is the one of UTM coordinates with an easting and a northing.
The coordinates within a UTM zone are metrical and perpendicular to each other.
The easting is preceded by the number of the UTM zone.
Our example, as a complete UTM zone coordinate, is represented as follows:
 • Easting: 32439596
• Easting: 32439596
• Northing: 5967780
The point is located in the UTM zone 32, which is based at the central meridian, 9 degrees eastern longitude.
Because the value 439596 is below 500000, the point is located exactly 60404 meters west of the central meridian (500000 m - 439596 m = 60404 m).
In northern direction, the point is exactly 5967780 meters perpendicular away from the equator.
TRANSDATpro allows the conversion of coordinates between thousands of Coordinate and Reference Systems.
The required Coordinate Reference System must be set by selecting parameters from the list boxes shown here.
UTM zone coordinates can be directly entered into the input fields of the program or can be read in from files.
The input of coordinates is possible with none or with up to nine decimal places.
The program formats the coordinates entered and to be calculated according to your requirements in the field "Decimals" (number of decimal places).
In the bottom list box, you can either select the natural UTM zone (indicated by its geographical longitude) or enforce the calculation into a defined zone.
Thereby, the UTM zone will be enlarged over its extension of 6 longitudes degrees.
The denomination "UTM zone" is equal to "meridian strip".
The enforcement of a certain UTM zone is therefore called "zone swap" or "meridian swap".
A zone swap is required, whenever a number of coordinates from different UTM zones are to be displayed jointly in one single zone or when they are subject of linear calculation.
An example is the representation of Germany (see figure), which spans both UTM zones 32 and 33.
If a zone swap to the eastern UTM zone 33 is enforced for our example coordinate of the beacon "Red Sand", we get the following result:
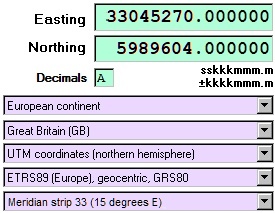 • Easting: 33045270
• Easting: 33045270
• Northing: 5989604
The point is now located in the UTM zone 33, which lies around the central meridian at 15 degrees eastern longitude.
Because the value 045270 is less than 500000, the point is located exactly 454730 meters west of the central meridian (500000 m - 045270 m = 454730 m).
In northern direction, now the point is exactly 5989604 meters perpendicular away from the equator.
If instead a zone swap to the western UTM zone 31 is enforced for our example coordinate, we get the following result:
• Easting: 31834124
• Northing: 5979368
The point is now in the UTM zone 31, which is around the central meridian at 3 degrees eastern longitude.
Because the value 834124 is greater than 500000, the point is exactly 334124 meters east of the central meridian (834124 m - 500000 m = 334124 m).
In northern direction, now the point is 5979368 meters perpendicular away from the equator.
You will have noticed that the northings in zones 31 and 33 differ from the northing in zone 32.
The difference is due to the fact, that in the rectangular UTM system the distance to the equator is measured on a parallel shift of the central meridian.
Because each UTM zone is represented as an individual Cartesian Coordinate System, the different northings between the different UTM zones are correct.
 For military purposes, UTM coordinates are represented in the "Military Grid Reference System" (MGRS) or "UTM Reference System" (UTMref).
To indicate the geographical latitude, the meridians are subdivided into UTM bands of 8 degrees along the parallels that are denominated with letters.
The UTM zones, in turn, independent of the UTM bands, are divided into squares with a lateral length of 100 km each, positioned parallel to the central meridian.
The UTM squares are denominated with letter pairs.
A point, exact to the meter, is notated with 5 digits of the east and of the north position, respectively, within the UTM square.
Again, we take the coordinates of the beacon "Red Sand":
For military purposes, UTM coordinates are represented in the "Military Grid Reference System" (MGRS) or "UTM Reference System" (UTMref).
To indicate the geographical latitude, the meridians are subdivided into UTM bands of 8 degrees along the parallels that are denominated with letters.
The UTM zones, in turn, independent of the UTM bands, are divided into squares with a lateral length of 100 km each, positioned parallel to the central meridian.
The UTM squares are denominated with letter pairs.
A point, exact to the meter, is notated with 5 digits of the east and of the north position, respectively, within the UTM square.
Again, we take the coordinates of the beacon "Red Sand":
• 32UME3959667780 Field exact to the meter
The point is located in the UTM zone 32.
It is the meridian strip with the central meridian at 9 degrees eastern longitude.
Also, the point is located in the UTM band U, which extends between 48 and 56 degrees northern latitude.
It is located as well within the UTM square ME, 100 km west of the central meridian and 5900 km north of the equator.
The position exact to the meter is 39596 meters east of the south western corner of the UTM square and 67780 meters north of the same.
The accuracy of a UTMREF coordinate can be varied by the (even) number of digits, in order to describe this way a larger or smaller area.
These are some examples with differing accuracy:

| • 32UME3959667780 | exact to the meter |
| • 32UME395677 | exact to 100 meters |
| • 32UME3967 | exact to 1 kilometer |
| • 32UME | exact to 100 kilometers |
The conversion program TRANSDATpro can calculate UTMref coordinates in different accuracy levels. The picture shows the necessary settings. Because UTMref coordinates are not described as usual with a northing and an easting, but are stored in only one single string, the second entry field remains empty.
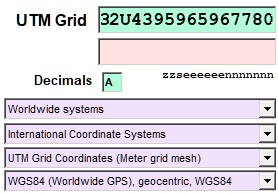
 UTM Grid Coordinates are represented in a slightly different way.
The UTM grid coordinate of the beacon "Red Sand" looks as follows:
UTM Grid Coordinates are represented in a slightly different way.
The UTM grid coordinate of the beacon "Red Sand" looks as follows:
• 32U4395965967780 UTM Grid Coordinate
The point is located in the UTM zone 32 and in the UTM band U.
The exact position is 60404 meters west of the central meridian (500000 m - 439596 m = 60404 m).
To the north, the point is at an exact distance of 5967780 meters perpendicular to the equator.
 It is quite simple to complete the UTM zone number 32 and the distance to the central meridian 439596 by hand to an easting 32439596 and use it together with the northing 5967780 as a UTM zone coordinate.
It is quite simple to complete the UTM zone number 32 and the distance to the central meridian 439596 by hand to an easting 32439596 and use it together with the northing 5967780 as a UTM zone coordinate.
On closer inspection, it can be seen that the UTM square, as used in the UTM Reference System, has simply been omitted from this representation form.
Without nominating the UTM square, the UTM band seems to be superfluous.
However, it is used for immediate identification of the hemisphere.
UTM Grid Coordinates are rarely used because UTM Zone coordinates and the UTM Reference System are better suited for dealing with UTM coordinates.
Unfortunately, the zone number is not always included in UTM zone coordinates.
This kind of representation of UTM coordinates is often used under the condition that the UTM zone is known.
In the easting the zone number is simply omitted thereby.
In fact, it is not an official notation but results from a certain degree of convenience.
Originally, the reason for the use of reduced coordinates was the computer technology.
Because of the memory requirements for large amounts of data and to reduce the effort, the zone numbers were omitted.
Another criterion was provided by the Army, which included a separate data field in its databases for the zone identifier (e.g., 32 or even 32U).
This also found acceptance in the civilian sector.
Our test coordinate might look as follows:
 • Easting: 439596
• Easting: 439596
• Northing: 5967780
In this case, the UTM zone has to be guessed, calculated or at least taken as a constant value.
The use of complete UTM coordinates should be preferred whenever possible.
Allegorically, incomplete UTM coordinates can be compared with house numbers where the street names are missing.
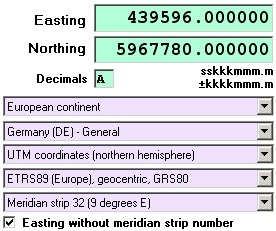
For this special case, the TRANSDATpro program provides an option to predefine an UTM zone respectively a meridian strip.
In the example the meridian strip 32 is selected as default from the 5th list box.
Thus, the easting 439596 is completed to 32439596.
Requirement for this approach is that the northing is completely like in this example.
For the target coordinate the output of the easting can be set optionally with or without UTM zone.
It also is possible to enforce the conversion to a particular UTM zone.
Sometimes the first digit of the northing (1000 kilometer digit) is also suppressed.
For the area of Germany it is always a 5, apart from a small area in the north of the country:
 • Easting: 439596
• Easting: 439596
• Northing: 967780
In this case, not only the UTM zone, but also the 1000 km digit of the northing must be known.
Therefore the program TRANSDATpro has the possibility to complete the coordinate with addends.
In the example, the addend for the easting is 32000000.
Thus, the value 439596 is complemented to 32439596.
The same applies for the northing, which is complemented to 5967780 by the addend 5000000.
From time to time, also multipliers are needed.
This applies for example, when using other measures then meters (like feet, yards or miles).
Behind the button "?!", there is a list box that includes the most common conversions.
With just one mouse click, you may convert the output of the Prussian Cadastre Coordinates from meters to "Prussian feet".
For more recent use: Also the American NAD27 coordinates can be directly converted into US Survey feet.
By entering the same Coordinate and Reference System for the source coordinates and for the target coordinates, the described reduced coordinates can be comfortably completed by means of addends.
TRANSDATpro was developed by the German company Killet GeoSoftware Engineering.
The geodetic program performs coordinate transformations with datum shift fast and with high accuracy.
It supports worldwide thousands of Coordinate Systems, geodetic Reference Systems and Datum Shifts, user-defined systems, 2D/3D transformations, INSPIRE, NTv2, HARN, EPSG, GPS, continental drift and more.
TRANSDATpro reads and writes the file formats Text, CSV, SDF, dBase, ArcShape, ArcGenerate, KML, GPX and others.
Among others, it offers Outdoor GPS reception, mapping in Google Earth, Google Maps and OpenStreetMap, Meridian Convergence, many Extra Parameter and a multilingual user interface.
For more detailed information, please go to our website  https://www.killetsoft.de/p_trda_e.htm.
https://www.killetsoft.de/p_trda_e.htm.
Developers of geodetic programs and applications may also access the Geodetic Development Kit GeoDLL which contains precise functions for topics like 2D and 3D coordinate conversions, change between datum or Reference Systems, meridian swaps, geodetic tasks, distance calculations, Digital Elevation Models as well as support of NTv2.
GeoDLL is distributed as DLL for 32bit and 64bit WINDOWS platforms and as source code in C / C++.
For more detailed information, please go to our website  https://www.killetsoft.de/p_gdla_e.htm.
https://www.killetsoft.de/p_gdla_e.htm.

 Dipl.-Ing. Fred Killet
Dipl.-Ing. Fred Killet
Killet GeoSoftware Ing.-GbR (KilletSoft)
Escheln 28a
47906 Kempen (Germany)
https://www.killetsoft.de
 In order that you are always well informed about our company, we write actual news, current information and special offers here into this column.
In order that you are always well informed about our company, we write actual news, current information and special offers here into this column.
 Read more...
Read more...
 Read more...
Read more...
 Description ORTWIN...
Description ORTWIN... Description TOPOWIN...
Description TOPOWIN...
 Register now...
Register now...
 Read more...
Read more...
 Read the work sheet...
Read the work sheet...
 Read the work sheet...
Read the work sheet...
 Read the work sheet...
Read the work sheet...
 Read the Press Release...
Read the Press Release... To the NTv2 collection...
To the NTv2 collection...
