2D / 3D Coordinate Transformations

With exception of the Cartesian coordinates, all Coordinate Transformations always are calculated using their underlying geographic Coordinate Systems. Both Cartesian and geographic Coordinate Systems contain the parameter of their Earth Ellipsoids.

A geographic Coordinate System can be 2D (two dimensional) or 3D (three dimensional). Coordinate Transformations in the 2D modus as well as in the 3D modus are based on both dimensions latitude and longitude. In a 3D Coordinate System, the additional third dimension is the ellipsoidal height, which means the height above the ellipsoid surface.

Cartesian coordinates are always done in the 3D modus. The Cartesian Coordinate System is based on three dimensions X, Y and Z, which mean the vector values of a point in meter

Compared with other transformation software GeoDLL as a special feature can also perform 3D calculations when using NTv2 files.

In the practical handling of 3D coordinate transformations the ellipsoidal height usually is problematic, because it is often not known. The ellipsoidal height must not be confused with the orthometric height (see notes further down). To show the effect of the height component on coordinate transformations, in the list below the geographical coordinate φ=53°03'07.59" / λ=10°28'38.99 for different heights is transformed to UTM / ETRS89.

Even with large height difference of several 100 meters, the horizontal displacement remains very low with a few millimeters.

Note: In case of missing ellipsoidal height, it is generally sufficient to do 2D transformations!

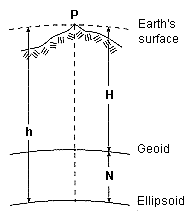
The ellipsoidal height denotes the shortest distance between a point on the earth's surface (ground point) and the earth ellipsoid associated to the Coordinate System. It may not be confused with the orthometric height, which is the distance of a point on the earth's surface to the earth geoid. The geoid depend on the gravitation field of the earth and corresponds to the Mean Sea Level. The difference between the ellipsoidal height and the orthometric height is referred as undulation. Thus, the ellipsoidal height is calculated as the sum of the orthometric height and the undulation. The ellipsoidal height is less suitable for surveying tasks. For this the orthometric height is more appropriate. With knowledge of the undulation N the orthometric height H of a point P can be calculated from the ellipsoidal height h. To determine the undulation you need a digital elevation model.

The orthometric height is calculatet by:

H = h - N

with:

N: Undulation

h: Ellipsoidial height

H: Orthometric height

hoehen

Orthometric heights are usually measured heights above the earth geoid. The geoid is characterized in that at each point of its surface gravity is equal and therefore theoretically on the geoid surface water can not flow. The geoid is fixed by a specified zero-height in its location to the earth surface. From country to country different zero-heights are defined. Examples of zero-heights are the "Normaal Amsterdams Peil" (NAP), the "Mean Sea Level" (MSL) and the "Normal-Null" (NN). If orthometric heights are available in addition to coordinates, that are to be transformed into a different coordinate reference system, they must and may not be converted by a 3D transformation. They keep their value in their zero-height system after the coordinate transformation as well.

Note: With coordinate transformations orthometric heights must not be converted.