2D / 3D-Koordinatentransformationen

Mit Ausnahme von kartesischen Koordinaten werden alle Koordinatentransformationen immer auf ihrem zugrundeliegenden geographischen Koordinatensystem ausgeführt. Sowohl kartesische als auch geographische Koordinatensysteme beinhalten die Parameter ihrer Erdellipsoide.

Ein geographisches Koordinatensystem kann 2D (zweidimensional) oder 3D (dreidimensional) sein. Koordinatentransformationen im 2D- und im 3D-Modus basieren auf den beiden Dimensionen Breite (latitude) und Länge (longitude). In einem 3D-Koordinatensystem wird zusätzliche als dritte Dimension die ellipsoidische Höhe, also die die Höhe über der Oberfläche des Ellipsoids, verwendet.

Kartesische Koordinaten werden immer im 3D-Modus ausgeführt. Das kartesische Koordinatensystem basiert auf den drei Dimensionen X, Y und Z, welche die Vektoren eines Punktes in Meter darstellen.

Als Besonderheit im Vergleich mit anderer Transformationssoftware kann GeoDLL auch bei der Verwendung von NTv2-Shiftdateien 3D-Berechnungen durchführen.

Bei der praktischen Handhabung von 3D-Koordinatentransformationen ist meist die ellipsoidische Höhe problematisch, da sie oft nicht bekannt ist. Die ellipsoidische Höhe darf dabei nicht mit der orthometrischen Höhe verwechselt werden (siehe Anmerkungen unten). Um den Einfluß der Höhenkomponente auf die Koordinatentransformation aufzuzeigen, wird nachfolgend die geographische Koordinate φ=53°03'07.59" / λ=10°28'38.99" für verschiedene Höhen nach UTM / ETRS89 transformiert.

Auch bei großer Höhendifferenz von mehreren 100 Metern bleibt die Abweichung in der Lage mit wenigen Millimetern sehr gering.

Hinweis: Bei fehlender ellipsoidischer Höhe reicht meist eine 2D-Transformation aus!

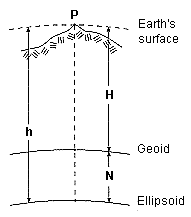
Die ellipsoidische Höhe bezeichnet den kürzesten Abstand zwischen einem Punkt auf der Erdoberfläche (Geländepunkt) und einem dem Koordinatensystem zugeordneten Erdellipsoid. Sie darf nicht mit der orthometrischen Höhe verwechselt werden, die den Abstand des Punktes auf der Erdoberfläche zum Erdgeoid darstellt .Das Geoid ist vom Gravitationsfeld der Erde abhängig und entspricht der mittleren Meereshöhe. Der Unterschied zwischen der ellipsoidischen und der orthometrischen Höhe wird als Undulation bezeichnet. Demnach ergibt sich die ellipsoidische Höhe aus der Summe der orthometrischen Höhe und der Undulation. Die ellipsoidische Höhe ist für Vermessungsaufgaben weniger geeignet. Dafür ist die orthometrische Höhe besser geeignet. Bei Kenntnis der Undulation N kann die orthometrische Höhe H eines Punktes P aus der ellipsoidischen Höhe h berechnet werden. Zur Ermittlung der Undulation benötigt man ein Höhenmodell.

Die orthometrische Höhe errechnet sich aus:

H = h - N

mit:

N: Undulation

h: Ellipsoidische Höhe

H: Orthometrische Höhe

hoehen

Hinweis: Für 3D-Transformationen müssen ellipsoidische Höhen verwendet werden!

Orthometrische Höhen sind in der Regel über dem Erdgeoid eingemessene Höhen. Das Geoid ist dadurch gekennzeichnet, dass auf jedem Punkt seiner Oberfläche die Schwerkraft gleich groß ist und deshalb theoretisch auf der Geoid-Oberfläche kein Wasser fließen kann. Das Geoid ist durch eine festgelegte Null-Höhe in seiner Lage zur Erdoberfläche fixiert. Von Land zu Land sind unterschiedliche Null-Höhen definiert. Beispiele für Null-Höhen sind der "Amsterdamer Pegel" (NAP), das Normalnull (NN) und der Mittlere Meeresspiegel" bzw. "Mean Sea Level" (MSL). Wenn zu Koordinaten, die in ein anders Koordinatenbezugssystem transformiert werden sollen, zusätzlich orthometrische Höhen vorhanden sind, müssen und dürfen sie nicht mittels einer 3D-Transformation umgerechnet werden. Sie behalten auch nach der Koordinatentransformation ihren Wert im Null-Höhen-System.

Hinweis: Orthometrische Höhen müssen bei Koordinatentransformationen nicht umgerechnet werden!